
I – INTRODUCTION
La numérisation est le procédé permettant la construction d’une représentation discrète d’un objet du monde réel. Dans son sens le plus répandu, la numérisation est la conversion d’un signal (vidéo, image, audio, caractère d’imprimerie, impulsion) en une suite de nombres permettant de représenter cet objet en informatique ou en électronique numérique. On utilise parfois le terme franglais digitalisation (digit signifiant chiffre en anglais).
Lorsqu’un son est enregistré à l’aide d’un microphone, les variations de pression acoustique sont transformées en une tension mesurable. Il s’agit d’une grandeur analogique continue représentée par une courbe variant en fonction du temps. Un ordinateur ne sait gérer que des valeurs numériques discrètes. Il faut donc échantillonner le signal analogique pour convertir la tension en une suite de nombres qui seront traités par l’ordinateur. C’est le rôle du convertisseur analogique/numérique Ainsi, la numérisation permet de transformer un signal sonore en fichier enregistré sur le disque dur de l’ordinateur.
La numérisation se réalise en deux étapes, l’échantillonnage et la quantification. Elle va permettre de transformer un signal continu en une suite de valeurs discrètes (distinctes) qui seront traduites dans le langage des ordinateurs, en 0 et 1.II – L’ ECHANTILLONNAGE
L’échantillonnage est le passage d’un signal continu en une suite de valeurs discrètes (discontinues).
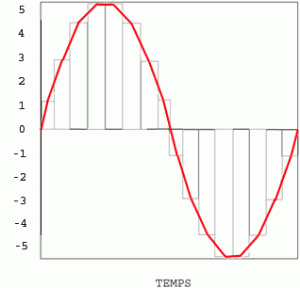 C’est la première phase de la numérisation qui consiste à passer d’un signal à temps continu en une suite de valeurs mesurées à intervalles réguliers. Le signal analogique est ainsi découpé en “tranches” ou échantillons (samples). Le nombre d’échantillons par seconde d’audio représente la fréquence d’échantillonnage ou sampling rate. Celle-ci est exprimée en Hertz (Hz).
C’est la première phase de la numérisation qui consiste à passer d’un signal à temps continu en une suite de valeurs mesurées à intervalles réguliers. Le signal analogique est ainsi découpé en “tranches” ou échantillons (samples). Le nombre d’échantillons par seconde d’audio représente la fréquence d’échantillonnage ou sampling rate. Celle-ci est exprimée en Hertz (Hz).
1 KHz = 1000 Hz
La fréquence d’échantillonnage d’un signal audio n’est pas choisie arbitrairement. Elle doit être suffisamment grande, afin de préserver la forme du signal. Le Théorème de Nyquist – Shannon stipule que la fréquence d’échantillonnage d’un signal doit être égale ou supérieure au double de la fréquence maximale contenue dans ce signal. Si la fréquence choisie est trop faible, les variations rapides du signal analogique ne seront pas enregistrées. Ainsi pour un fichier de qualité téléphonique, on échantillonnera à 11,025 KHz – 8 bits – mono. Cela permettra de traiter des fréquences allant jusqu’à 5500 Hz, ce qui est largement suffisant pour rendre une voix parfaitement compréhensible.
Pour un enregistrement audio en qualité CD, la bande passante étant généralement de 20 KHz, on échantillonnera à 44,1 KHz – 16 bits – stéréo.
Dans un projet audio, pour la réalisation d’un CD de musique par exemple, on choisira dès le départ une résolution de 24 bit et une fréquence d’échantillonnage de 44.100 kHz (ou un multiple pair de cette fréquence 88.2 kHz , 176.4 kH). Les fréquences d’échantillonnage de 48 KHz, 96 KHz ou 192 Khz sont plutôt utilisées dans des projets vidéo et ne donnent pas le meilleur résultat lors de la conversion finale en 44.100 kHz. On verra plus loin dans ce dossier, la technique du dithering pour passer à une résolution numérique inférieure. Naturellement, la place occupée par notre fichier sur le disque dur sera fonction de la qualité choisie.Ces graphiques montrent l’influence de la fréquence d’échantillonnage :
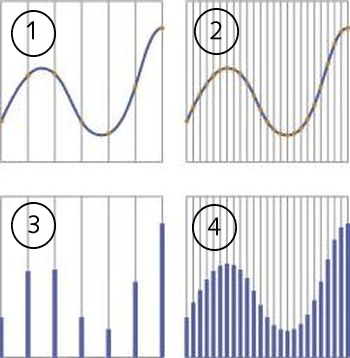
Les figures 1 et 2 représentent les signaux analogiques.
Les figures 3 et 4 montrent ces mêmes signaux après numérisation.
On notera que le signal est dans les 2 cas codé sur le même nombre de bits.
Dans la figure 4 la fréquence d’échantillonnage du signal analogique est le quadruple de celle utilisée en 3.On constate que plus la fréquence d’échantillonnage est élevée, plus le signal numérique se rapproche de la définition du signal analogique.
III – LA QUANTIFICATION
C’est la seconde phase de la numérisation. Après avoir découpé le signal continu en échantillons, il va falloir les mesurer et leur donner une valeur numérique en fonction de leur amplitude. Pour cela, on définit un intervalle de N valeurs destiné à couvrir l’ensemble des valeurs possibles. Ce nombre N est codé en binaire sur 8-16-20 ou 24 bits suivant la résolution du convertisseur A/N. L’amplitude de chaque échantillon est alors représentée par un nombre entier.
Codage sur 8 bits = 2 puissance 8 = 256 valeurs possibles
Codage sur 16 bits = 2 puissance 16 = 65536 valeurs possibles
Codage sur 20 bits = 2 puissance 20 = 1.048.576 valeurs possibles
Codage sur 24 bits = 2 puissance 24 = 16.777.216 valeurs possibles.
Nous donnons ci-dessus le nombre de valeur possibles que peut prendre un échantillon. Cela signifie qu’en 16 bits cette valeur varie entre 0 et 65535 (en réalité en audio entre -32768 et +32767) et en 24 bits entre 0 et 16 777 215 (en réalité entre – 8 388 608 et + 8 388 607).
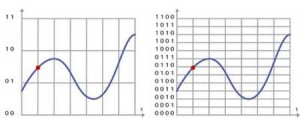 A gauche codage sur 2 bits : la valeur attribuée au point rouge sur la courbe est 01
A gauche codage sur 2 bits : la valeur attribuée au point rouge sur la courbe est 01
A droite codage sur 4 bits : on peut attribuer à ce même point une valeur plus précise 0110
Le signal audio est maintenant numérisé. Notons que nombre de bits définit aussi l’amplitude dynamique du signal (6 dB/bit). Un équipement ayant une résolution de 16 bits offrira une dynamique maximale de 16*6=96 dB, pour une résolution de 8 bits, 8*6=48 dB. Plus l’encodage sera puissant, plus la dynamique sera élevée et le bruit de fond limité.
Rappel sur le codage binaire
On associe à chaque bit un poids. Ce poids est fonction de la position du bit dans l’octet.
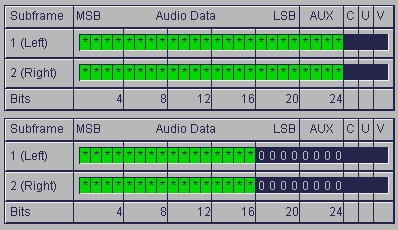
LSB : (Least significant Bit) bit de poids faible, c’est le bit qui a le moins de signification dans un octet. Par convention, c’est le bit le plus à droite dans l’écriture d’un mot. Exactement comme dans le nombre 105, c’est le chiffre le plus à droite qui à le moins de poids, la valeur la plus faible.
MSB : (Most significant bit) bit de poids fort, c’est le bit qui a le plus de signification dans un octet. Par convention, c’est le bit le plus à gauche dans l’écriture d’un mot. Exactement comme dans le nombre 105, c’est le chiffre le plus à gauche qui à le plus de poids, la valeur la plus forte.
IV – LE DITHERING
4.1 – Le principe du dithering
Le dithering est une forme de bruit blanc utilisé pour réduire les artefacts de quantification dans les systèmes audionumériques. Ce procédé s’applique lors de traitements audio ou d’enregistrements numériques avec réduction du pas de quantification (24 à 16 bits par exemple) . Ces distorsions sont particulièrement audibles dans les passages de faible niveau sonore ou dans les fadeout. Au final, ce bruit est perçu comme un souffle constant, superposé au signal. Il est parfois à peine audible, en tout cas bien moins que la distorsion de quantification qui serait apparue sans dithering. Le dithering est donc un compromis entre les performances en termes de rapport signal/bruit et l’existence évidente d’artefacts. Son utilisation appropriée permet en tout cas de tirer des performances maximales de toute résolution de destination. Sans dithering, un signal 44100/16/2 à un rapport S/B d’environ 96 à 100dB. Avec un dithering, on peut aller à plus de 110dB !
Les logiciels audionumériques offrent aujourd’hui une variété de solutions basées sur des algorithmes internes spécifiques ou des des plugins externes. Citons parmi les produits les plus célèbres, l’ UV22HR d’Apogee ou l’ IDR de Waves.
4.2 – Le Noise Shaping
Le noise shaping est une technique de mise en forme du bruit pour améliorer encore plus les performances audio. Il utilise le filtrage numérique pour réduire le bruit qui se trouve au milieu du spectre audio. C’est en effet dans la bande de fréquences située autour de 4 KHz que l’oreille humaine est la plus sensible. En réalité, ce bruit n’est pas réduit, mais il est déplacé dans la partie haute du spectre de fréquences où il est nettement moins perceptible. Après cette mise en forme, le bruit se retrouve décalé dans des régions où notre oreille l’entend beaucoup moins que sous sa forme originale (dynamique augmentée pour frq <10 KHz, dynamique réduite pour frq >10 KHz).
Pour le paramétrage du noise shaping, vous devez naturellement vous référer à la notice de votre logiciel. A titre indicatif voyez ci-dessous un descriptif relevé dans la notice “Pro Tools Guide des plug-in DigiRack” :
Type 1 : Possède le spectre de fréquence le plus plat dans la gamme des fréquences audibles, modulant et accumulant le bruit de dithering juste en dessous de la fréquence Nyquist. Recommandé pour les sons d’une faible complexité stéréophonique tels que les enregistrements d’instruments solo.
Type 2 : Possède une courbe de noise shaping d’ordre faible optimisée psychoacoustiquement. Recommandé pour les sons d’une plus grande complexité stéréophonique.
Type 3 : Possède une courbe de noise shaping d’ordre élevé optimisée psychoacoustiquement. Recommandé pour les sons couvrant tout le spectre audible, répartis dans tout l’espace stéréo.
4.3 – Quand doit-on appliquer le dithering ?
Le Dithering doit être appliqué dès que l’on passe à une résolution numérique inférieure. Une des utilisations les plus courantes consiste à l’employer comme dernier processeur sur la sortie master d’un mix lorsque vous préparez une session 24 bits pour le mastering CD.
Certains logiciels audionumériques travaillent avec une résolution interne de 32/64 bits virgule flottante, ce qui garantit une excellente qualité audio. Cela signifie que tous les traitements en temps réel appliqués aux données audio (correction de niveau, mixage, effet) se feront dans cette résolution et non en 16 bits. Un Dithering doit donc être appliqué en sortie pour revenir en 16 bits.
4.4 – Paramétrage d’un plugin
En matière de paramétrage, il n’existe pas de règle universelle simple. Tout dépend de la qualité des données audio originales. Il est vivement recommandé de tester les différents types de dither et options de noise shaping offerte par votre logiciel pour trouver le réglage qui convient le mieux à votre oreille ! Le réglage ” Quantize” ou “Bit Resolution” permet de régler la résolution maximale de votre destination 8, 16, 20 ou 24 bits.
En résumé !
On peut s’étonner que l’ajout d’un léger bruit de fond améliore la qualité du son. En fait, lorsque l’on réduit la résolution d’un son numérisé (de 24 bits à 16 bits, par exemple), on est obligé de réduire la quantité d’informations codant chaque échantillon. La valeur de chaque échantillon est donc à nouveau calculée pour être casée sur 16 bits, et son résultat devient décimal. Comme on ne code que des entiers sur 16 bits, une solution consisterait à tronquer la valeur de chaque échantillon. Cela donne de très mauvais résultats sonores, là où le dithering en donne de très bons. On utilise aussi le dithering lors des conversions A/N.
V – QUELQUES INFORMATIONS COMPLEMENTAIRES
Le CD Audio
Ce “bon vieux” support date de 1979 ! En qualité CD, le son est analysé 44100 fois par seconde (d’où la fréquence 44,1 KHz) en mesurant chaque fois ses caractéristiques sur une échelle de 16 bits offrant 65536 valeurs possibles.
Le DVD Audio
C’est la norme définie par le DVD Forum (échantillonnage à 192 KHz – quantification sur 24 bits). Le résultat final donne plus de 1000 fois plus d’informations musicales que sur le CD !
Le SACD
Il s’agit d’un format plus “propriétaire” promu par SONY et PHILIPS. Le procédé est différent puisque, cette fois, le son est analysé près de 3 millions de fois (2.822.400) par seconde sur 1 bit.
Le DVD Audio et le SACD augmente considérablement la quantité d’informations par rapport au CD. Cela se traduit par une durée plus importante des musiques stéréo ou par l’augmentation du nombre de canaux. Ainsi on obtient un son 5.1 sans compromis ! Mais pour le moment, ces systèmes sont très peu présents sur le marché. Il faudra certainement revoir les prises de son, inventer de nouvelles musiques ou de nouvelles créations audiovisuelles pour pouvoir réellement profiter de toutes ces possibilités et qualités !

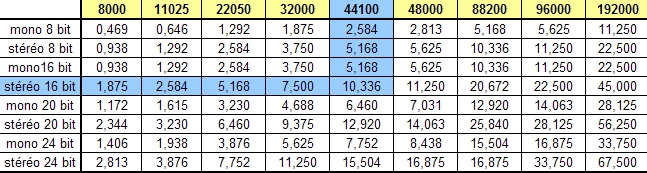 Le tableau ci-dessus montre l’espace disque à prévoir en Mo pour un enregistrement audio d’une minute en format wav. Ces données correspondent à des valeurs approximatives, mais elles montrent bien la nécessité d’utiliser des formats audio compressés sur le Web.
Le tableau ci-dessus montre l’espace disque à prévoir en Mo pour un enregistrement audio d’une minute en format wav. Ces données correspondent à des valeurs approximatives, mais elles montrent bien la nécessité d’utiliser des formats audio compressés sur le Web.