Physique du Son
I – INTRODUCTION

Les sons sont des phénomènes vibratoires qu’on peut classer en 3 catégories selon leur perception ou non par l’oreille humaine :
Les sons audibles ont une fréquence comprise entre 20 Hz et 20 KHz (*). Les sons inaudibles BF ou infrasons ont une fréquence inférieure à 20 Hz. Les sons inaudibles HF ou ultrasons ont une fréquence supérieure à 20 KHz. Les sons qui parviennent à nos oreilles résultent donc de vibrations de l’air. Sous une excitation mécanique produite par un instrument de musique ou une personne qui parle, l’air se met à vibrer. Une molécule reçoit alors une impulsion qui la met en mouvement dans une direction donnée. Sur son parcours, elle rencontre d’autres molécules qu’elle pousse, formant ainsi une zone de compression. L’air possède une certaine élasticité, il ne tarde donc pas à se détendre. La matière traversée par l’onde acoustique est alors le siège de compressions et de dépressions successives et périodiques. Ce phénomène crée une onde progressive longitudinale.
Ces mouvements se propagent à une vitesse qui dépend du milieu (élément traversé) et des conditions (température, pression). Dans l’air calme, sous une pression atmosphérique normale et à 20° C, la vitesse de propagation du son est de 340 m/s. Dans un milieu homogène, les vibrations se propagent uniformément dans toutes les directions, mais elles finissent par s’amortir progressivement. L’amortissement est d’autant plus important que la fréquence est élevée. En conséquence, les sons aigus portent moins loin que les sons graves à intensité égale. On sait maintenant pourquoi nos voisins n’aiment pas nos chaînes HIFI.
Pour que le son se propage, la présence d’un milieu élastique est indispensable : le son ne se propage pas dans le vide. Ajoutons également que les molécules vibrent sur place. Un son sortant d’un haut-parleur n’a jamais créé de courant d’air !
(*)
Hz = Hertz
KHz = KiloHertz
MHz = MégaHertz
1 Hz = 1 vibration/seconde
1 KHz = 1000 Hz
1 MHz = 1000 KHz = 1000000 Hz
II – LES FREQUENCES AUDIBLES
Ces oscillations ne deviennent un son que parce qu’elles agissent sur nos sens et plus particulièrement notre oreille qui est sensible aux vibrations comprises entre 16 et 20.000 oscillations par seconde. Le nombre de vibrations complètes en 1 seconde détermine la fréquence. Celle-ci est exprimée en Hertz – symbole Hz – (1 KHz = 1000 Hz). En dessous de 16 Hz, les infrasons sont perçus par la paroi abdominale. Cette propriété est largement utilisée par l’industrie du cinéma pour la réalisation de certaine bandes sonores. Au dessus de 20.000 Hz, il s’agit d’ultrasons perçus par certains animaux (cf. dressage des chiens au moyen de sifflets ultrasonores). Cette limite supérieure varie en fonction des individus et de leur âge. Les enfants entendent jusqu’à 20.000 Hz, puis, cette limite supérieure diminue à mesure que l’âge augmente. Les adultes ne dépassent pas 15.000 Hz et les personnes âgées 12.000 Hz. Ces limites s’appliquent naturellement aux personnes qui ont une “bonne oreille”.
III – PHENOMENE OSCILLANT PERIODIQUE
L’ébranlement de l’air produit par un son pur, comme celui du diapason, est un phénomène oscillant périodique qui est représenté par une fonction sinusoïdale de la forme :
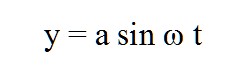
Le phénomène étant cyclique, on peut le représenter par un point qui se déplace sur un cercle avec une vitesse uniforme; le cercle est entièrement décrit lorsque le point parcouru un angle de 2pi. donc 2pi/T représente la vitesse de déplacement du point sur le cercle.
IV – LES SONS SIMPLES ET SONS COMPLEXES
 Ce graphique représente un son simple ou “pur”, mais ce cas est très rare. En effet, la plupart des sources sonores produisent des sons complexes qui sont constitués par une fréquence fondamentale sur laquelle se superposent des harmoniques et des transitoires. Les harmoniques sont des multiples entiers de la fréquence fondamentale. On distingue les harmoniques pairs (2f, 4f, 6f, 8f…) et les harmoniques impairs (3f, 5f, 7f, 9f…). Les sons sont donc formés d’une superposition de vibrations ayant des amplitudes très variables dont la courbe résultante est très irrégulière. Le théorème de Fourier permet de démontrer qu’un signal complexe peut être décomposé en une série de signaux sinusoïdaux simples. Les transitoires sont constitués à l’établissement ou l’extinction d’un son d’une manière brusque comme par exemple les percussions, les cymbales, ou l’attaque d’une note de piano. Les transitoires ne sont pas décomposables en série de Fourier.
Ce graphique représente un son simple ou “pur”, mais ce cas est très rare. En effet, la plupart des sources sonores produisent des sons complexes qui sont constitués par une fréquence fondamentale sur laquelle se superposent des harmoniques et des transitoires. Les harmoniques sont des multiples entiers de la fréquence fondamentale. On distingue les harmoniques pairs (2f, 4f, 6f, 8f…) et les harmoniques impairs (3f, 5f, 7f, 9f…). Les sons sont donc formés d’une superposition de vibrations ayant des amplitudes très variables dont la courbe résultante est très irrégulière. Le théorème de Fourier permet de démontrer qu’un signal complexe peut être décomposé en une série de signaux sinusoïdaux simples. Les transitoires sont constitués à l’établissement ou l’extinction d’un son d’une manière brusque comme par exemple les percussions, les cymbales, ou l’attaque d’une note de piano. Les transitoires ne sont pas décomposables en série de Fourier.
V – LES CARACTERISTIQUES D’ UN SON
Un son est défini par 3 paramètres : sa fréquence, son amplitude, et son timbre. Toutes les opérations que réalisent les logiciels de traitement du son tournent autour de ces 3 caractéristiques.
L’intensité
L’intensité d’un son correspond à l’amplitude de la vibration acoustique. En d’autres termes, elle caractérise le volume sonore qui nous permet de distinguer un son fort d’un son faible.
La hauteur
La hauteur d’un son est liée à la vitesse de vibration de l’air, c’est-à-dire la fréquence. Les variations de la fréquence fondamentale permettent de situer un son sur l’échelle des graves et des aigus. Le spectre audible (16 à 20000 Hz) est divisé en octaves qui couvrent un intervalle de fréquences dans un rapport de 1 à 2. La fréquence de référence est représentée par la note la3 dont la valeur a été fixée à 440 Hz.
Le timbre
Le timbre est donné par les harmoniques et les transitoires qui accompagnent la fréquence fondamentale. Il permet de différencier deux sons de même hauteur et de même amplitude. C’est ainsi que l’on reconnaîtra, à l’oreille, deux instruments de musique jouant une même note ou une personne qui parle. Le timbre est constitué d’un ensemble fréquences appelé spectre. La richesse du spectre permettra de dire qu’un son est riche, brillant, profond …
VI – LA PERCEPTION DES SONS
6.1 – La pression acoustique
Nous savons maintenant que le son résulte d’une variation périodique de la pression de l’air . Les ondes produites transmettent une certaine quantité d’énergie. Dans le Système International (SI), l’unité de pression est le Newton par mètre carré (N/m²) nommé en France le pascal (Pa). L’atmosphère est à environ 1020 hPa.
6.2 – Le diagramme de Fletcher et Munson
 Les courbes classiques de Fletcher et Munson mettent en relation la fréquence et la puissance sonore. Elles donnent ainsi la sensibilité moyenne de l’oreille en fonction de la fréquence. Lorsque l’on applique un signal sonore d’intensité croissante, l’oreille ne perçoit ce signal qu’à partir du seuil d’audibilité (courbe I). Puis l’oreille perçoit l’augmentation progressive d’énergie jusqu’à un niveau où l’audition devient douloureuse. L’oreille est saturée et aucune augmentation de sensation n’est plus perceptible. Le seuil de douleur est atteint (courbe II). Ce diagramme montre également que notre oreille est plus sensible aux fréquences médiums situées entre 500 et 5000 Hz (l’oreille est plus adaptée à la parole, notre principal moyen d’expression !). Les lignes intermédiaires relient les points du diagramme pour lesquels la sensation de volume est égale. Ces courbes résultent d’une étude statistique et correspondent donc à une oreille “moyenne”. Dans la réalité, ces valeurs dépendent de nombreux facteurs comme par exemple l’âge ou l’état de santé d’un individu.
Les courbes classiques de Fletcher et Munson mettent en relation la fréquence et la puissance sonore. Elles donnent ainsi la sensibilité moyenne de l’oreille en fonction de la fréquence. Lorsque l’on applique un signal sonore d’intensité croissante, l’oreille ne perçoit ce signal qu’à partir du seuil d’audibilité (courbe I). Puis l’oreille perçoit l’augmentation progressive d’énergie jusqu’à un niveau où l’audition devient douloureuse. L’oreille est saturée et aucune augmentation de sensation n’est plus perceptible. Le seuil de douleur est atteint (courbe II). Ce diagramme montre également que notre oreille est plus sensible aux fréquences médiums situées entre 500 et 5000 Hz (l’oreille est plus adaptée à la parole, notre principal moyen d’expression !). Les lignes intermédiaires relient les points du diagramme pour lesquels la sensation de volume est égale. Ces courbes résultent d’une étude statistique et correspondent donc à une oreille “moyenne”. Dans la réalité, ces valeurs dépendent de nombreux facteurs comme par exemple l’âge ou l’état de santé d’un individu.
6.3 – Le décibel
La sensibilité de l’oreille n’est pas linéaire car la sensation varie comme le logarithme de l’excitation. Pour doubler la sensation acoustique il faut multiplier par 10 la puissance sonore. C’est pourquoi on utilise le décibel pour définir le niveau acoustique par rapport au seuil de sensibilité. Le décibel (dB) est la dixième partie du Bel. C’est l’unité de mesure du niveau sonore.
6.4 – Mesure du niveau de pression acoustique
Pour la mesure des niveaux de pression acoustique on adopte comme niveau de référence la pression acoustique nécessaire pour atteindre le seuil d’audibilité à 1000 Hz qui a été fixé à 2.10-5 Pa. Cela correspond à 0 dB SPL Sound Pressure Level. Le niveau d’audition d’un sujet pour un son donné est exprimé en dB SL Sensation Level. Comme il peut varier selon le moment et l’état physiologique du sujet, cela ne signifie pas qu’un niveau dB SL corresponde nécessairement au niveau dB SPL.
Pref = 2.10–5 Pa
dB SPL = 20 Log10 (P/Pref)
Dans de nombreux calculs les lettres SPL ou SL ne sont pas ajoutées, c’est dommage. Les dB SPL permettent aussi de calculer le niveau acoustique à une certaine distance de la source sonore. Si on admet se trouver dans des conditions de propagation sphérique, la pression est inversement proportionnelle à la distance de la source. En d’autres termes, le niveau de pression décroît de 6 dB à chaque fois que la distance double.
On trouve aussi parfois des valeurs exprimées en dB (A). Il s’agit d’un décibel pondéré ou physiologique. Un filtre est appliqué à la source sonore pour éliminer les basses et hautes fréquences qui sont peu ou pas perçues par l’oreille. Le dispositif se comporte alors comme une oreille moyenne. Les sonomètres, appareils qui mesurent les niveaux d’intensité sonore, sont conçus suivant ce principe. Ils sont généralement utilisés pour mesurer le niveaux des bruits dans l’environnement.
VII – VITESSE DE PROPAGATION DU SON
L’onde acoustique se propage dans l’air à 340 m/s, dans l’eau à 1500 m/s et à des vitesses encore supérieures dans les matériaux plus denses (3500 m/s dans l’os et jusqu’à 6000 m/s dans l’acier!). Dans le vide, dépourvu de matière, aucun son ne se propage.
Exemple : si on met une source sonore sous une cloche, on entend le son. En revanche, si on fait le vide sous la cloche, le son disparait puisqu’il n’y a plus de molécules d’air.
D’autres facteurs tels que le taux d’humidité, la température influencent la vitesse de propagation de l’onde.
VIII – QUELQUES ELEMENTS DE THEORIE
Log(y puissance x) = x log(y)
Log(x) + Log(y) = Log(xy) et Log(x) – Log(y) = Log(x/y).
Log(x) = y si et seulement si x = 10 puissance y. Le logarithme décimal n’est défini que pour x > 0
Log(10) = 1. Puisque 10 = 10 puissance 1
Log(1) = 0
Pour 0<x<1, Log(x) < 0 ce qui explique les dB négatifs !
Donc [A x B]dB = [A]dB + [B]dB mais [A+B]dB n’est pas égal à [A]dB + [B]dB
Exemple 1
Calculons le niveau en dB d’une source dont la pression acoustique est de 1 Pa.N dB = 20 Log (1/2.10 puissance -5) = 20 Log 50000 = 20 x 4.7 = 94 dB.
Tous les domaines liés à l’électronique font largement appel au dB. Comme indiqué au paragraphe 6.5, il s’agit d’une valeur relative qui nécessite toujours une référence 0 dB. Pour distinguer ces références, un suffixe est ajouté derrière les lettres dB. Ainsi, vous trouverez des dBu, dBV, dBm, dB FS très employés dans le domaine audio.
Exemple 2
Prenons l’exemple d’une machine dont le niveau sonore est de 80 dB(A). Si l’on met en route une seconde machine identique le niveau sonore n’est pas égal à 160 dB(A) car les niveaux sonores ne s’additionnent pas comme des unités classiques. En fait, si l’énergie double, le bruit n’augmente que de 3 dB…Le niveau sonore des 2 machines est donc de 83 dB(A).
Page publiée le : 07/04/2014
Dernière modification : 27/05/2020
Voir les CGU
